Ezekiel's Wheen Calculations

Math is great, but actual physical tests are better if you can simulate the working principles closely enough. There may be (and I suspect there are) things going on that the math isn’t taking into account.
Once you understand (and can physically prove) the working principles, you can do fine tuning to make an efficient machine… Maybe even one that is practical OU.

Here are some thoughts to address what I consider to be the main issues:

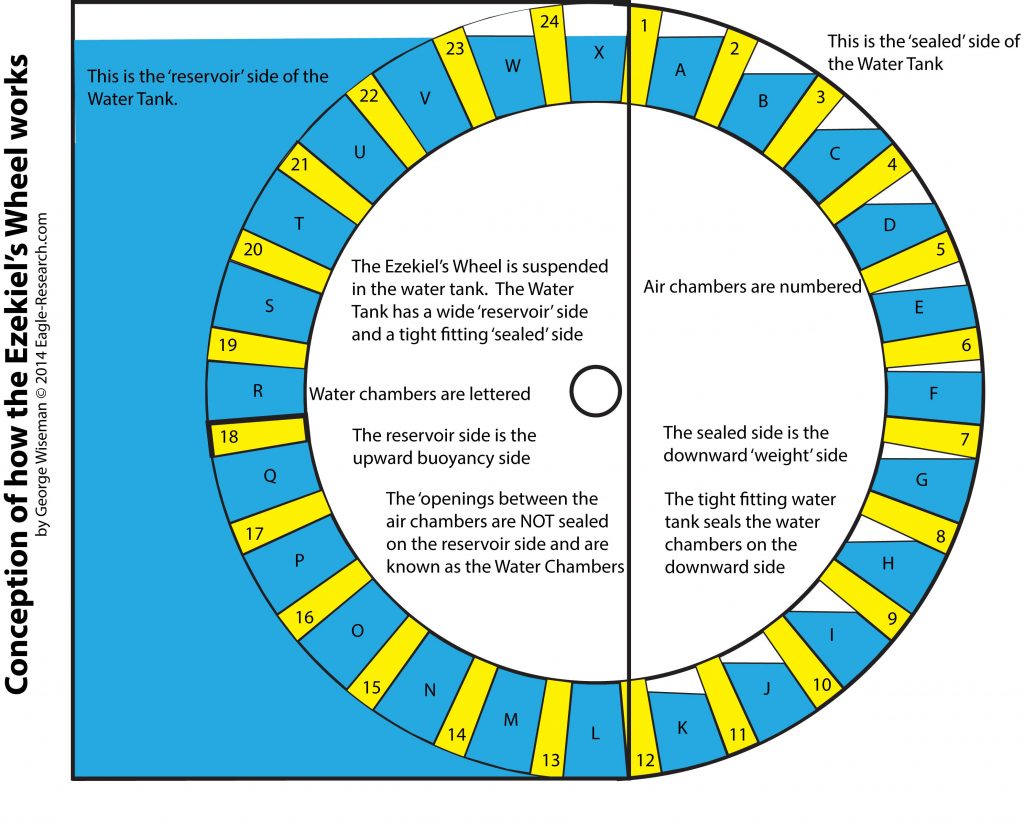
One of the things needed with any technology is setting standards so that people can talk to each other without confusion. Once there are standards, various tests and comments can be compared. BTW, one person called it the EZ wheel; I liked that.
The biggest issue to overcome is the torque needed to force the air chambers into the water reservoir. Here is an experiment that’ll help people understand the ‘water pressure’ issue… And try various things to reduce the pressure or help the wheel move against it.

Ezekiel's Wheel Buoyancy / Weight 'Start Torque' Test

This is where some innovation is still required. I have some ideas, which I’ll introduce shortly. Anything we can do here will increase the efficiency of the wheel.

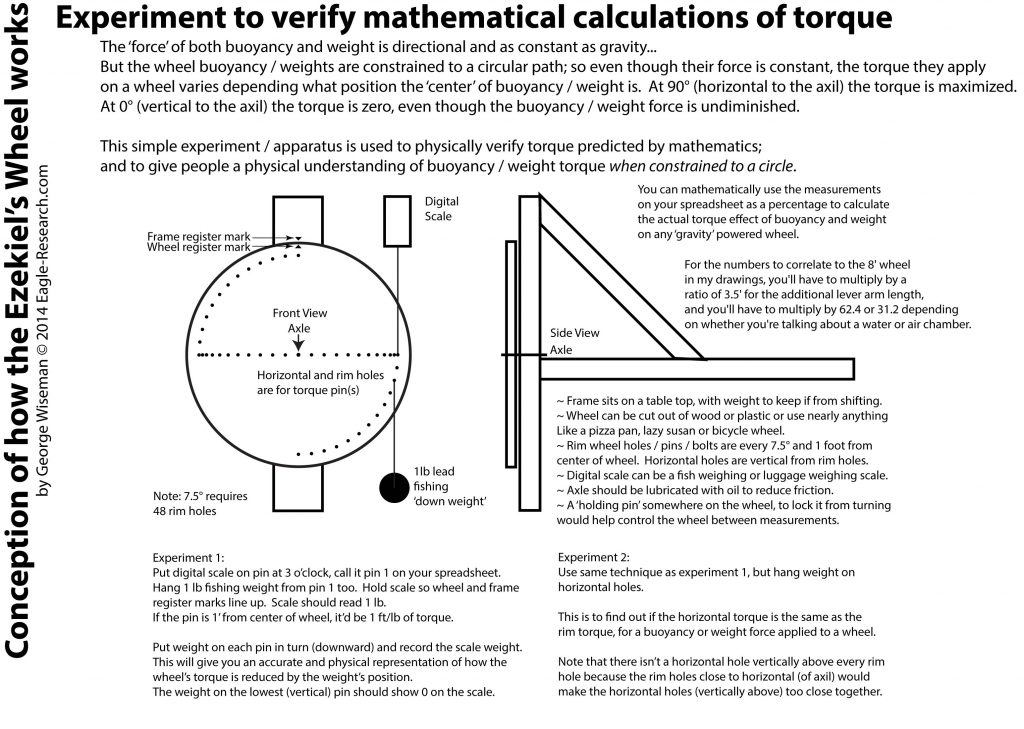
Some people (including me) have trouble conceptualizing mathematical equations and sometimes the math is miss-applied or incorrect for the forces involved. Here’s a simple apparatus / experiment that’ll help people ‘get it right’ and perhaps ‘see’ things that will help.

Like I can see that most of the wheel’s torque occurs in about a 60° range, 30° above and below horizontal. Buoyancy and weight have much less effect on the wheel’s power output above or below this ‘torque range’.

Soooo maybe… if we configure the wheel’s seals (and maybe water reservoir) so that the reservoir’s water pressure can pressurize (be common) up to 30° on the downward side, then the air chambers are entering the reservoir at a higher water level, where there is less water ‘back-pressure’.

Yes, we lose some torque on the downward side but it’s less effective torque anyway and we also lose back-pressure against the wheel.
Also the buoyancy ‘back-torque’ on the downward side will be compensated by the buoyancy on the upward side; so except for friction, I think we end up with a net gain.

It may even be that this effect is already happening naturally in the real wheel, with the 1/16th inch clearances allowing limited water leakage, ‘filling’ and pressurizing the lower chambers on the downward side. The pre-pressurization would allow the air chambers to enter the main reservoir with less back-pressure.

1. As for which side of the axle the water reservoir should be on. I see no great advantage to torque either way, so I like the idea of having the axle out of the reservoir.

2. Yes, you do lose water out of the water chambers as they rise out of the water reservoir, but in my concept of ‘lowering the water level’ I specifically FILL the water chambers with a horizontal tube/pipe/channel that is on the outside of the wheel, at about the ‘D’ level.

Lowering the water level reduces the back-pressure without seriously affecting the Ezekiel’s Wheel torque, because (as you’ll see if you do the torque experiment) any buoyancy / weight beyond 30° above and below the horizontal to the axle quickly reduces to zero.

3. It also occurs to me, that since the most effective torque the wheel generates is in the 30° range above and below the horizontal of the axle, that keeping the water chambers SEALED (away from reservoir pressure) until they reach about ‘P’ on the wheel, may also mitigate the reservoir water pressure since the air chambers would be entering the reservoir at that higher level.

This would be a great modification to the ‘water pressure’ experiment (hole in the side of the bucket plugged with a cork). I’m not sure what would be the best method to represent this aspect/idea… Maybe just lower the water level in the bucket appropriately?

A combination of the two above ideas would allow the water weight to generate torque on the downward side from about ‘D’ to ‘G’, the area between ‘H’ and ‘O’ would be pretty much neutral, buoyancy would take over at about ’17’ and generate torque until about ’20’ and the wheel would be neutral over the top.

‘Reverse’ water pressure would be the water pressure from ‘high level’ (about ‘T’) to the entry at about ’17’. So we’d be having maximum torque with minimum back-pressure.

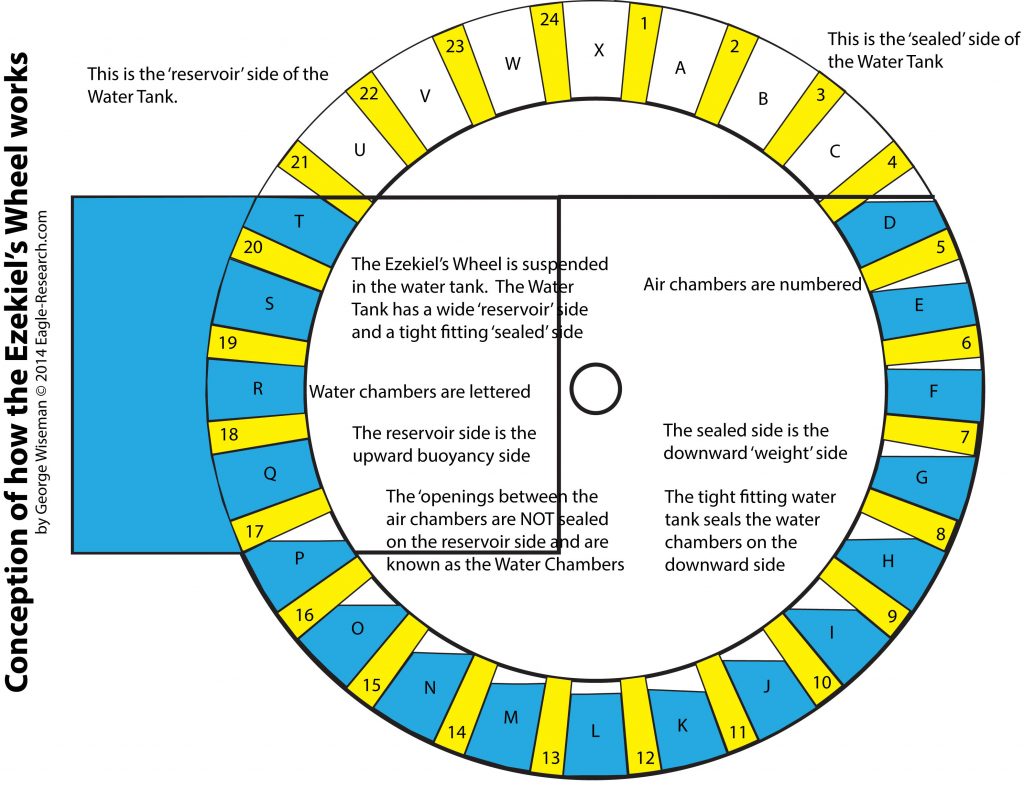
Here’s a drawing of the concept. In this case the water tank stays sealed to the wheel until the wheel enters the bottom of the reservoir… And there is an exterior horizontal water channel at the top, leading from the reservoir to the sealed side, which I didn’t depict.

Calculating Torque.

Online torque calculator
http://frictionhinge.com/calc.html

Torque of a water wheel
http://24volt.eu/eng_kalkyl_vridmoment.php

Water Wheel torque formulas
http://ffden-2.phys.uaf.edu/211_fall2010.web.dir/Brooks/water-wheel-physics.html

FAQ: What is Buoyancy?

http://www.newton.dep.anl.gov/askasci/phy05/phy05225.htm

http://www.hp-gramatke.net/pmm_physics/english/page0550.htm

https://www.physicsforums.com/threads/gravity-force-and-buoyancy.5208/

Archimedes Wheel
http://www.nuenergy.org/generator-driven-by-a-buoyancy-engine/

Finding center of gravity and center of buoyancy.

http://www.planetseed.com/mathsolution/floating-and-stability-center-buoyancy

http://www.engineeringtoolbox.com/centre-gravity-buoyancy-d_1286.html